往年题库
一、简答
- 什么是马尔科夫过程?马尔科夫过程满足泊松分布的前提是什么?
- 什么是拜占庭错误?什么是拜占庭一致性?
- **z(t), f(t), R(t), F(t)是什么,有什么关系?**为什么z(t)描述部件故障比f(t)好?
- 码距与检错数和纠错数什么关系?检错和纠错的基本原理是什么?
- 可修复性对可靠性和可用性有什么作用?
- 什么是同步时钟协议?举例说明同步时钟协议的必要性。
- TMR在什么情况下比单个部件的可靠性高?TMR的MTTF是多少?
二、大题
- 叙述拜占庭协议。画出n=7,m=2的情况。
- 叙述确定性时钟同步协议。
- 画出与右边RBD相对应的故障树,计算可靠性(p)。
- 叙述捎带确认协议。
- 右下图Adaptive DSD算法,从1开始,求每一轮TESTED_UP和STATE数组。
- 叙述三阶段提交协议,说明为什么3PC是无阻塞协议。
- 计算2个部件热备份的可靠性,计算可修复时的可用性。
- 计算下图n=3时的可靠性,其中部件可靠性为 ,投票器可靠性为 。
Tips:加粗为25年真题
解答
1. 什么是马尔科夫过程?马尔科夫过程满足泊松分布的前提是什么?
马尔科夫过程是指状态变量为离散的、时间变量为连续的随机过程。其基本特性是无记忆性,即系统从当前状态转移到下一状态的概率仅依赖于当前状态,与过去的状态序列无关。
马尔科夫过程满足泊松分布需满足以下三个前提条件:
单位时间内发生一次转移的概率为 ,其中 是常数,表示单位时间内发生的平均次数,且事件是不可逆的,发生次数不会减少。
每次事件的发生是相互独立的,任一事件的发生不依赖于其他事件。
在足够小的时间间隔 内,发生两次或以上事件的概率可以忽略不计。
2. 什么是拜占庭错误?什么是拜占庭一致性?
拜占庭错误:在分布式系统中,节点发生错误时的行为是不可预知的,甚至会向不同节点发送完全不同的信息。
拜占庭一致性:拜占庭协议中所有无故障节点能够保持一致,使用相同的值。
(正确性:当发送节点无故障时,所有无故障节点与发送节点一致。)
3. z(t), f(t), R(t), F(t)是什么,有什么关系?为什么z(t)描述部件故障比f(t)好?
设 为系统部件总数, 是 时刻系统中正常的部件数量,则
可以得到
z(t)代表系统运行到t时刻后相对于当时的故障率,能清晰反映故障率的变化趋势;而f(t)代表系统在t时刻相对于整体的故障率,不容易直接识别故障模式。
4. 码距与检错数和纠错数什么关系?检错和纠错的基本原理是什么?
设码距为d,检错数为D,纠错数为C,则满足以下公式
当一个码落在两个合法码字中间,说明出错,能检错的比特数小于码距;
当错误码在两个码字中间更靠近一个合法码字,就可以纠错,因此码距要大于两倍的纠错数。
5. 可修复性对可靠性和可用性有什么作用?
可靠性要求系统在一定时间t内无故障运行,可用性要求系统在t时刻无故障。因此在单部件系统中,可修复性可以提高可用性,对可靠性没有帮助。
6. 什么是同步时钟协议?举例说明同步时钟协议的必要性。
分布式时钟同步协议是指在分布式计算系统中,通过一定机制确保各节点的时钟信息保持一致的过程,准确的时钟同步信息确保了系统的可靠性和数据的一致性。
eg. 若时钟不同步,在交易时可以利用两地不同步的时钟用同一笔钱给两地转账获利。
7. TMR在什么情况下比单个部件的可靠性高?TMR的MTTF是多少?
TMR的可靠性 ,单个部件可靠性为 ,通过 得到在 时,TMR比单个部件的可靠性高。
,所以可靠性
利用公式:
得到:
1. 叙述拜占庭协议。画出n=7,m=2的情况。
- ICA(0)
- transmitter将它的值发给其他节点
- 每个节点使用从transmitter得到的值,如果没有则使用默认值。
- ICA(m)
- transmitter将值发送给其他 n-1 节点
- 节点 i 作为 ICA(m-1) 的transmitter将接收到的 发送给其他 n-2 个节点,如果没有则发送默认值
- 对每个节点 i,将从节点 j 收到的值作为 ,使用 作为自己的值
2. 叙述确定性时钟同步协议。
假设时钟漂移受限于 的情况下,为了解决双面时钟的问题,需要满足2个条件:
- 任意两个非故障进程对同一时钟的读取值近似相等
- 若 是非故障时钟,则所有非故障时钟必须能读到 的近似正确值。
由此得到同步算法的数学模型 ,即无法调整物理时钟的情况下,调整CORR使得每台机器的逻辑时钟近似相等。
假设所有时钟最开始已经被同步到了大致相同的值,且相差不超过 :
在一个进程j达到 时,其他进程会在不超过 的真实时间到达 ,设进程之间的延迟在 之间,且时钟漂移限制于 ,那么进程j可以确定会在不晚于 的时间内收到其他进程的信息。
最多可能存在 个故障时钟,因此进程在获得的所有时钟值中,去掉最大f和最小f个时钟后取中间值(平均数)作为新的时钟。
3. 画出与右边RBD相对应的故障树,计算可靠性(p)。
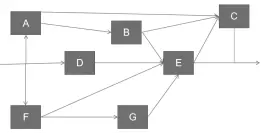
min tieset = {A, C}, {D, E}, {F, E}, {A, B, E}
min cutset = {A, D, F}, {A, E}, {C, E}, {C, D, F, B}故障树的树根是多个cutset集合的OR,每个集合求AND
可靠性对min tieset求并集:
4. 叙述捎带确认协议。
- 每个节点维护4个列表,分别为
ack-list,nack-list,received-list,PR-list。 - 当节点要发送消息
m时,将ack-list,nack-list追加到m中作为m.acks,m.nacks,重置ack-list并广播m,同时广播PR-list的消息。若一段时间没有收到肯定确认,就将m加入PR-list。没有消息要发送,就构造一个空消息来携带确认消息。 - 当节点接收消息
m时,- 将
m.id添加到ack-list中,将m转存received-list中。若在nack-list中发现m.id,或在PR-list中发现m,就删去对应列表的消息; - 检查
m.acks,从ack-list中删除所有匹配的id,将所有匹配id但自身未接收到的消息加入nack-list; - 检查
m.nacks,若存在received-list匹配的消息,则将其加入PR-list中,否则加入nack-list。
- 将
5. 叙述Adaptive DSD算法,并对下图从1开始,求最后一轮节点1的TESTED_UP和STATE数组。
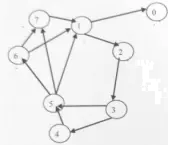
- 节点在列表中按顺序循环排列,例如1, 2, …, n, 1.
- 节点i依次测试i+1, i+2…直到找到一个无故障节点。
- 找到无故障节点t后,停止测试,并记录
TESTED_UPi[i]=t,表示t由i直接测试并判定无故障;复制TESTED_UPt的数据,更新到自己的TESTED_UP中。 - 诊断信息沿测试路径逆向传播,使得整个系统的节点能够逐步获得正确诊断信息。
TESTED_UP1 = [x, 2, 3, 5, x, 1, x, x]
STATE = [0, 1, 1, 1, 0, 1, 0, 0]6. 叙述三阶段提交协议,说明为什么3PC是无阻塞协议。
- 在投票阶段,协调者向所有参与方发送提交请求,参与者进行本地检查,成功则回复YES,否则回复NO并进入中止状态。
- 如果所有响应都是YES,协调者本地也是YES,则协调者向所有参与者发送PREPARE,进入准备提交状态,否则发送ABORT报文;参与者收到PREPARE后发送ACK并进入提交状态,收到ABORT报文终止事务处理
- 收到所有ACK报文后协调者向所有参与者发送COMMIT报文,参与者收到COMMIT报文后完成提交协议。
3PC不包含与丢弃(ABORT)状态和提交(COMMIT)状态同时相邻的本地状态 ,也不包含与提交(COMMIT)状态相邻的非可提交状态,因此可以在有站点发生故障时也不导致其他造作站点阻塞。
7. 计算2个部件热备份、可修复时的可靠性和可用性。
8. 计算下图n=3时的可靠性,其中部件故障率为 ,投票器故障率为 。
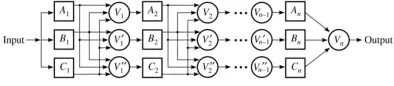
设 的可靠性为 ,投票器的可靠性为 ,则
经过第一次投票,得到每一个投票器的可靠性, 的可靠性就是 ,以此类推,第二次投票和第三次投票后的可靠性分别为 , . 所以整体可靠性为 .
附录
微分方程 $y’ +p(x)y=q(x) $ 的通解:
设 ,则有
带入 ,即 时刻初始状态的概率为 ,其他状态的概率为 ,解出 的值。
常见的 .
免责声明
仅为个人笔记,不提供备考建议和指南