引例

先举个例子，小张从家到公司上班总共有三条路可以直达（如下图），但是每条路每天拥堵的可能性不太一样，由于路的远近不同，选择每条路的概率如下：

$P(L_1)=0.5,P(L_2)=0.3,P(L_3)=0.2$

每天上述三条路不拥堵的概率分别为：

$P(C_1)=0.2，P(C_2)=0.4,P(C_3)=0.7$

假设遇到拥堵会迟到，那么小张从 $\mathcal{Home}$ 到 $\mathcal{Company}$ 不迟到的概率是多少？

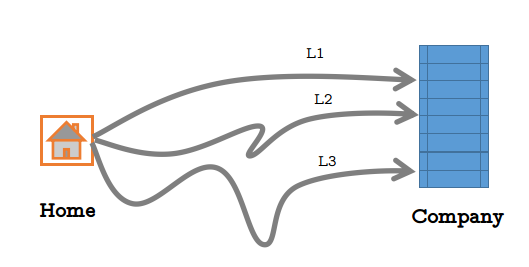
其实不迟到就是对应着不拥堵，设事件Ｃ为到公司不迟到，事件为选择第i条路，则：

$$ \begin{aligned} P(C)&=P(L_1)\times P(C|L_1) + P(L_2)\times P(C|L_2)+P(L_3)\times P(C|L_3)\\ &=P(L_1)\times P(C_1) + P(L2)\times P(C_2)+P(L_3)\times P(C_3) \end{aligned} $$

全概率就是表示达到某个目的，有多种方式（或者造成某种结果，有多种原因），问达到目的的概率是多少（造成这种结果的概率是多少）

全概率公式：

设事件 $L_1, L_2 \cdots L_n$ 是一个完备事件组，则对于任意一个事件 $C$ ，若有如下公式成立：

$$ \begin{aligned} P(C)&=P(L_1)\times P(C|L_1) + P(L_2)\times P(C|L_2)+\cdots +P(L_n)\times P(C|L_n) \\ &= \sum^n_{i=1} P(L_i)P(C|L_i) \end{aligned} $$

那么就称这个公式为全概率公式。

麻球繁衍

题意

一个麻球只能存活一天，这天他有 $p_i$ 的概率产生 $i$ 个后代（ $0 \leq i < n$ ）现在你有 $k$ 个麻球，求 $m$ 天之后全部死亡的概率（在这之前全部死完也算）。

思路

我们设事件 $L_0, L_1\cdots L_{n-1}$ 分别为产生 $0, 1\cdots n - 1$ 个后代， $C$ 为全部死亡的概率，则 $P(L_i)=p_i$ ，每一天麻球是否死亡相互独立，即 $C$ ~ $B(p, n)$

设 $f(i)$ 为 $1$ 只麻球 $i$ 天内死亡的概率，则 $P(C|L_i)=f(i-1)^j$

由全概率公式

$$ \begin{aligned} f(i)&=p_0+p_1f(i-1)+p_2f(i-1)^2+\cdots+p_{n-1}f(i-1)^{n-1}\\ &=\sum^{n-1}_{j=0}p_jf(i-1)^j\\ \end{aligned} $$

所求答案即为 $f(m)^k$

Code

cpp

#include <iostream>
#include <iomanip>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <algorithm>
using namespace std;
int n, k, m;
double p[1005], f[1005];
int main()
{
	cin >> n >> k >> m;
	for(int i = 0; i < n; i++)
		cin >> p[i];
	f[1] = p[0];
	for(int i = 2; i <= m; i++)
		for(int j = 0; j < n; j++)
			f[i] += p[j] * pow(f[i - 1], j);
	cout << fixed << setprecision(7) << pow(f[m], k);
return 0;
}

引例 ​

全概率公式： ​

麻球繁衍 ​

题意 ​

思路 ​

Code ​

引例

全概率公式：

麻球繁衍

题意

思路

Code